Продолжение табл. 21

Это выражение есть уравнение параболы.

Для определения скорости точки находим проекции скорости на оси координат:

o = i = 4 см/С; Vy = y31t см/с.

Модуль скорости точки

= /i + « (3)

Аналогично проекции ускорения точки

и) = = 0; Шу = ц = Ъ2 cм/c Модуль ускорения точки

w = Vw% + wl32 см/с

Координаты точки, а также ее скорость, ускорение и их проекции на координатные оси для заданного момента времени =1/2 с приведены в табл. 22.

Таблица 22

Касательное ускорение находим путем дифференцирования модуля скорости (3):

При ?=1/2 с

dv 4.0+16.32 ,j

Следовательно, модуль касательного ускорения

ш = 31 см/с

Знак «+» при dv/dt показывает, что движение точки ускоренное и, следовательно, направления и f совпадают.

Нормальное ускорение точки в данный момент времени

w„ = vw-wi = 1/32-312 - 7,94 т/с\

Радиус кривизны траектории в той точке, где при =1/2 с находится точка М,

р = у2/ш„ = 16,57,94 = 34,3 см.

Полученные значения ш, ш„ и р также приведены в табл. 22.

Пользуясь уравнением (2), строим траекторию (рис. 72) и показываем на ней положение точки М в заданный момент времени. Вектор v строим по составляющим и vy, причем этот вектор долиен быть направлен по касательной к траектории точки. Вектор w находим как по составляющим и wy, так и по и w„, чем контролируется правильность вычислений.

Дополнение к заданию /(-/. Уравнения движения точки на плоскости (табл. 21) можно использовать и для задания движения точки в пространстве, если дополнительно к табл. 21 задать третье уравнение z = z(t), которое приведено в табл. 23.

Пример выполнения задания. Исходные данные (в см и с):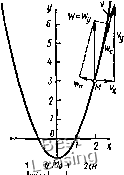

1/ = -4/-4; г = 2/ + 2; = 0.

7 а г h s 8 шм1с

и..... Ill , ,

5 О 5 1015 го iscnd

Ш 111 I-1

Рис. 72

Решение. Уравнения (4) являются параметрическими уравнениями траектории точки в пространстве. Исключая параметр / из первого и второго уравнений этой системы, а также из второго и третьего, находим:

ху = -\6; (5)

y = -2z. (6)

Уравнение (5) выражает в плоскости хОу равностороннюю гиперболу, для которой оси координат служат асимптотами. В пространстве этому уравнению соответствует гиперболический цилиндр с образующими, параллельными оси Ог.

Таблица 21

Уравнение (6) выражает в плоскости уОг прямую, проходягцую через начало координат, а в пространстве - плоскость, содержагцую ось Од:,

Траектория точки представляет собой линию пересечения этих двух поверхностен: гиперболического цилиндра и плоскости (рис. 73).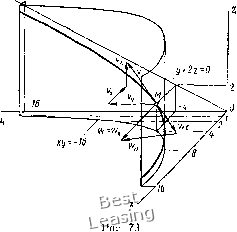

Проекции скорости точки на оси координат:

v.--=x =

v, = ij = - A см/с; V, = 2 = 2 см/с.

см/с;

Модуль cKopociH

v= \ vl-\-vl-Ьу; = f 4-Ь5 (Н-1) см/с.